最新!一号台风或将生成
1712 2025-05-14 09:33
高校实验室管理水平是数据水平指在高校建设不断深入,实验室建设的挖掘硬件条件逐渐改善,以及软件条件不断改进的校实情况下,衡量、验室评价实验室硬件和软件的管理相关管理程度。
数据挖掘是模型指利用算法将隐藏在大量、真实数据中的数据水平信息提取出来的过程,其属于一种深层次的挖掘数据分析方法,表现形式多种多样。校实例如,验室统计类数据挖掘包括回归分析、管理多变量分析等;知识发现类的模型数据挖掘包括支持向量机、规则发现、数据水平决策树等。挖掘
当下高校实验室管理水平的校实衡量和评估存在很多客观因素,因此实验室的管理水平评价模型有很多,例如:文献构建的基于缺陷塔模型与WNB的高校实验室安全评价分类模型,该模型的建立是以缺陷塔模型作为依据,并与权重朴素贝叶斯结合完成评价;文献构建的基于TOPSIS和DEA的评价模型,采用基于信息熵的理想解排序法和数据包络分析的综合评价模型实现评价。但是上述方法仅能够实现实验室在安全方面和效率方面的评估,对于实验室的体制管理、仪器设备管理以及规章制度管理等方面的评价无法实现。因此,为了更好地完成对这些相关管理水平的评价,本文构建数据挖掘的高效实验室管理水平评价模型,从而更全面、更有效地完成对实验室的管理水平评价。
选用密度峰值发现聚类算法完成实验室管理数据聚类。该算法对样本数据局部密度采用K近邻信息完成数据更新,使发现数据集的密度峰值、确定类簇中心点及类簇个数的准确性大幅度提高。为了完成聚类中心建模,该算法选择两个变量,分别为局部密度ρ和相对最小距离δ,用其描述样本数据,点与点的距离都与两个变量存在关联性,则样本数据i的局部密度ρi的表示公式为:
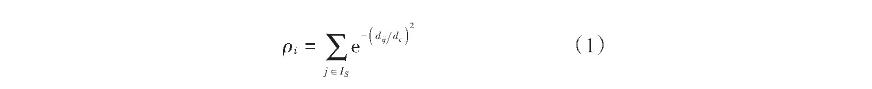
式中:dij为样本数据i与样本数据j之间的距离;dc为截断距离;IS表示样本数据集。
样本数据i与局部密度高于i的样本数据之间的最小距离被称之为相对最小距离,用δi表示,其表达式为:
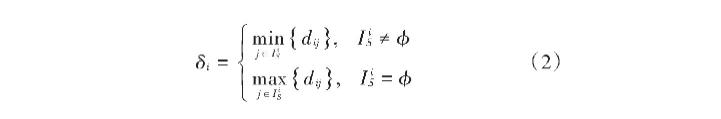
式中,假如样本数据i拥有最大局部密度值,则IiS≠ϕ,此时δi表示样本数据i与其他样本数据之间的最大距离,确保样本数据的最大局部密度值和相对最小距离值均维持最大。
通过计算数据集中每个样本数据,获取两个变量值后,采用下述步骤完成数据聚类:
1)类簇中心的确定需要找到密度高峰值点。
2)将剩余样本数据划分到类簇中,其为比剩余样本局部密度大且距离最小的样本数据所属的类簇。
3)针对使用决策图很难判断的情况,构建局部密度和相对最小距离结合参考量γ,γi=ρiδi,通过γi值的大小判断样本数据i是否为类簇中心,其值越大,样本数据i是类簇中心的可能性越大。因此,只要采用降序排列完成每个样本数据的γ值的处理后,选取相对较大γ值的样本数据为类簇中心。
类簇中心确定后,为完成实验室管理数据集聚类,需要将剩余数据划分至类簇中,该划分是根据局部密度逐渐降低的顺序实现;划分至类簇为密度比其高并且距离最小的样本数据所在的类簇。该算法具体流程为:
输入:数据集
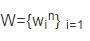
其包含n个数据。
输出:k个簇。
1)样本数据i的局部密度值ρi通过式(1)计算得到。
2)样本数据xi的相对最小距离δi通过式(2)计算得到。
3)绘制决策图需要根据ρi和δi完成,它们分别是各样本数据的局部密度值以及相对最小距离值,类簇中心是决策图中最优样本数据,是决策图中显著的、局部密度高和相对最小距离大的样本数据。
4)向最优样本对象中分配剩余样本数据,实现实验室数据集聚类。

声明:本文所用图片、文字来源《现代电子技术》,版权归原作者所有。如涉及作品内容、版权等问题,请与本网联系删除。
相关链接:实验室,样本,评价